Published Book on Amazon
| All of IOT Starting with the Latest Raspberry Pi from Beginner to Advanced – Volume 1 | |
| All of IOT Starting with the Latest Raspberry Pi from Beginner to Advanced – Volume 2 |
출판된 한글판 도서
| 최신 라즈베리파이(Raspberry Pi)로 시작하는 사물인터넷(IOT)의 모든 것 – 초보에서 고급까지 (상) | |
| 최신 라즈베리파이(Raspberry Pi)로 시작하는 사물인터넷(IOT)의 모든 것 – 초보에서 고급까지 (하) |
Original Book Contents
23.2.3 How to use Mathematica
Here we will use the case to explain how to use “notebook” in Mathematica.
23.2.3.1 How to Write Program in Mathematica
● Entering and executing script
In “Notebook” window, click the screen and type the following. Press [Shift + Enter] to execute the command. It prints "Hello world" on the screen as shown below.
| Print["Hello world"] |

You can do mathematical calculations by typing something that needs calculation in the following format.
| In[2]:= 2 + 2
Out[2]= 4
In[3]:= 16254 / 32
Out[3]= 8127 / 16
In[4]:= 1024 * 32
Out[4]= 32768 |
● Editing “Notebook”
You can modify, add or delete the previous entered command by clicking it with mouse or moving with [Up/Down Arrow] key, and can execute the command again by pressing clicking [Shift + Enter] in its place.
You can open the previously saved “Notebook” again, and you can see that all the input and output contents are the same as before, you can execute each cell again with [Shift + Enter], you can execute all at once by selecting the menu Evaluation à Evaluate Notebook.
● Using variable
During program processing, you can store the calculation results in a variable if necessary. Enter as follows. Note that typing semicolon “;” at the end of each line prevents output from printing.
| radius = 5; diameter = 2 * radius; circumference = 2 * Pi * radius; area = Pi * radius^2; |
● Symbolic values
In the below, let's look at the built-in symbol “Pi” that has a symbolic constant value for “π”. When we enter "Pi" in equation, this means that a reference to the true value for “π” has been passed to equation and it is not rounded to the decimal point.
| In[19]:= Pi
Out[19]: π
In[20]:= tau = 2 * Pi
Out[20]: 2 π |
If you want to know the decimal representation of the symbolic constant, use “N” function
| In[5]:= N[Pi]
Out[5]: 3.14159 |
Default significant figures for the symbolic constant are 6 digits. So the above result is 6 numbers. If necessary, you can also specify a higher precision for the second argument, as shown below.
| In[6]:= N[Pi, 10]
Out[6]: 3.141592654 |
The precision specified here is the total number of digits. In the above, it can be seen that the decimal point 9 is displayed together with number “3”.
● Lists
Collections of data can be stored in a list.
| nums = {1, 2, 3, 5, 8} people = {"Alice", "Bob", "Charlotte", "David"} |
● Range
You can easily create a list of number using “Range” function.
| Range[5] (*The numbers 1 to 5*) Range[2, 5] (*The numbers 2 to 5*) Range[2, 5, 2] (*The numbers 2 to 5, in steps of 2*) |
● Table
“Table” function can create new list data using the values of a list.
| Table[i ^ 2, {i, 10}] (*Squares of the numbers 1 to 10*) Table[i ^ 2, {i, 5, 10}] (*Squares of the numbers 5 to 10*) Table[i ^ 2, {i, nums}] (*Squares of the items in the list nums*) |
● Looping
You can run a loop a specified number of times or over the items in a list with “Do” function.
| Do[Print["Hello"], {10}] (*Print "Hello" 10 times*) Do[Print[i], {i, 5}] (*Print the numbers 1 to 5*) Do[Print[i], {i, 3, 5}] (*Print the numbers 3 to 5*) Do[Print[i], {i, 3, 5}] (*Print the numbers 1 to 5, in steps of 2*) Do[Print[i ^ 2], {i, nums}] (*Print the square of each item in the list nums*) |
● Function Help
If you put a question mark “?” in front of the function name and execute [Shift + Enter], you can get usage help for the function. Next is checking the help for function “Sqrt”.
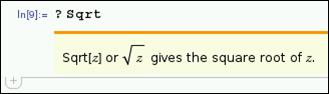
● Function Search
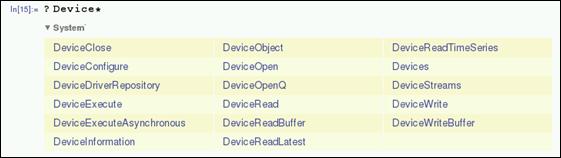
If you do not know a function name correctly, you can retrieve the list of functions matching the search condition at once by using a part of the function name and asterisk “*” as a wildcard together with question mark “?”. Below is the result of finding all the functions that contain the letter "Device" in the name.
| In[15]:= ?Device* |
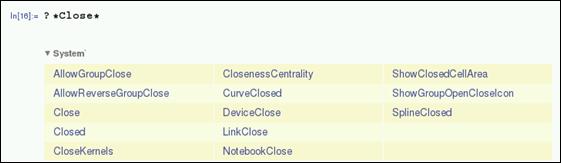
You can also use multiple wildcards as shown below. You will then be able to retrieve all the functions that meet the conditions.
| In[16]:= ?*Close* |
● Comments
You can annotate them in scripts in the format of “(*comment*)” using parentheses “( )” and asterisk “*”. These are ignored when the command is actually executed later.
| Print["Hello"] (*Print "Hello" to the screen*) |
23.2.3.2 Saving and Reusing Program
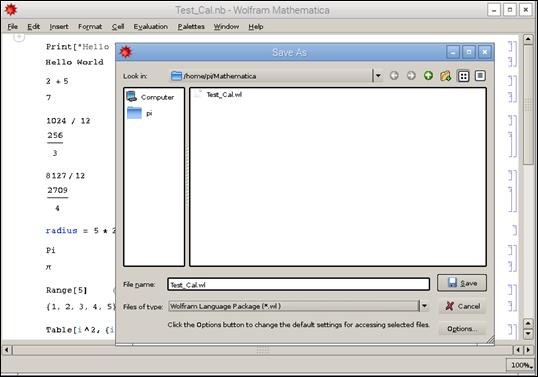
Once created, the program can be saved as a file using menu File à Save and reused. There are several formats available for saving it to a file. It can be saved as Wolfram notebook (.nb), Wolfram mathematica package (.m), Wolfram language package (.wl), or regular text file (.txt).
The data stored in a file can be re-opened and executed as it is or can be executed after modification. You can run each cell by using [Shift + Enter] or you can run the entire at once by selecting Evaluation à Evaluate Notebook in the menu.
● Running script in Shell with Wolfram
The scripts stored in Wolfram mathematica package (.m) or Wolfram language package (.wl) can also be executed directly from Shell using “wolfram” command, where “-script” flag must be used. In the following example, a script with “print” command is saved to “test_print.m” file. If you want to execute the script file directly from shell, execute as follows. This will print "Hello World" on the screen.
| wolfram -script test_print.m |
